一元二次方程求根公式(一元二次方程求根公式是谁发明的)
一元二次方程求根公式(一元二次方程求根公式是谁发明的)
众所周知,一元二次方程本属于初中的数学知识,其解法有配方法,因式分解法,公式法等。各类方法中,配方法有其硬核的讨论,公式法有其复杂的造型,还有飘逸的因式分解法,其神秘的气质令初中生又爱又恨!一元二次方程的解法已然成为数学基础的基础,如此基础的的方法竟然在21世纪又诞生了新解法,势必会赚足了眼球!

“一元二次方程新解法”的发明人叫罗伯森,是卡内基梅隆大学华裔数学教授、美国奥数教练,并且罗伯森教授表示:“如果这种方法直到今天都没有被人类发现的话,我会感到非常惊讶,因为这个课题已经有4000年的历史了,而且有数十亿人都遇到过这个公式和它的证明。”
事实上,在古代,全世界的数学家对一元二次方程都有研究,虽然也没有一模一样的方法出现,但是究其内涵,有些古代的解法与罗教授的解法可谓是大同小异。原因也不难想,古代的数学家们没有韦达,更没有代数的符号记法,而现如今罗教授的解法确实有“踩肩膀”的嫌疑。那么这个方法到底含金量多高,我们不做量化的评断,不妨为大家带来一场一元二次方程的解法PK,我们一起来欣赏一下古今数学大神的精彩表演。
2019年的新解法
有请第一位选手登场,掌声欢迎罗教授!为了更加形象直观,我们通过一个例子来说明该方法。
对于一元二次方程:X-8X+12=0,先假设该方程的根是R和S。
那么必会有:X-8X+12= X-R X-S。
将右侧展开得:X-8X+12=X- R+SX+RS。
左右对应相等,得:R+S=8;RS=12。
关键的部分来了,由于刚刚得到它们的和是8,则R和S的平均数是4,故方程的根可设为4+K,4-K,又因为RS=12,则 4+K 4-K=12,则16-K=12,则K=2 -2也是一样的结果,从而得到方程的两个根,4+2=6和4-2=2。方程解完!对于二次项系数不是1的情况,就先把二次项系数化为1,然后再进行以上操作。

当这个解法公之于众之后,各地纷纷发来声音,有人说这个解法简直太好了,再也不用死记硬背那个变态的公式了,再也不用苦苦的寻找那个配方的小尾巴了。当然也有来自中国学生的声音:这不就是十字相乘法嘛,解个方程哪要这么多步,我们需要的不是如何解方程,而需要如何短时间,正确的解方程!还有人认为,这就是韦达定理的小应用而已,并且韦达定理的表现形式要更为一般化。
无论如何,我们不得不佩服罗教授思维的新颖性,可谓“旧知识”和“新逻辑”的巧妙结合!
古阿拉伯的解法
提到古阿拉伯数学,不得不提一个重量级人物--阿尔花剌子模。“代数”一词本源于公元825年的一本用阿拉伯语写的书名,其作者就是花剌子模。没错,他就是我们今天登场的第二位选手。实话实说,当第一次看到罗教授的解法的时候,本人第一时间想到的就是阿尔花剌子模,这个阿拉伯人对方程的理解简直是登峰造极!

阿尔花剌子模在书中提出一个问题:“一个平方和十个这个平方的根等于三十九个迪拉姆,它是多少?”是不是看起来太绕了?由于当时代数符号根本没有发明,古代数学的方程只能靠文字去描述,我来帮大家解释一下,设这个数是X,那么“平方”就是X,“平方的根”就是将X在开方,故“平方的根”是指“X”,“十个这个平方的根”就是10X,问题转化为求方程:X+10X=39的解。 不得不佩服数学符号对数学的意义,如此简短的符号和冗长的文字形成了鲜明的对比!
花剌子模给出的解法是: 注意:下文中的“根”,不指现如今方程的根,而指平方根
①将根的个数减半。本题中,是将10减半,故得到5;
②用5乘自己,再加39,得到64;
③取64的根,即将64开方,得到8;
④再从中减去根的个数的一半,即再用8去减5,得到3,方程解完。
有些小朋友发现了问题,因为一元二次方程的根有2个,这都丢解了啊!莫要慌张,大数学家怎么能犯这么低级的错误呢,由于当时的人们普遍不接受负数,自然没有考虑负的情况。如果可以出现负数,那么在③的时候,将64开方,直接得到8,然后再都去减5,自然得到了两个根,3和﹣13。今天借用历史传统,我们这里仍然不谈负数的情况,指考虑平方根的正根情况。
下面对花剌子模的解法套上今天算式:
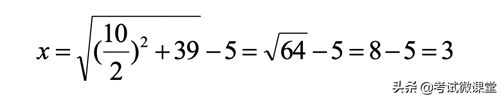
我们也可以看出,花剌子模所研究的方程就是二次项系数为1的二次方程,即x+bx+c=0,把上述方程的解法套上系数为字母的情况:
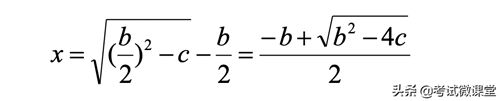
如果考虑到正负两个平方根,再考虑到二次项系数不为1的情况,这就是现代版的求根公式!
当第一次看到花剌子模方程解法的时候,本人是非常的不淡定,这种解法怎么能够想到呢?简直太需要脑洞了,不仅我这么想,相信与他同时代的人也都有此疑问,所以花剌子模并没有止步于此,他觉得应该为大家做出一个合理解释,于是他想到了一个证明方法,并且考虑到其他同仁的知识水平,这个方法必须大家都能接受,事实上,他找到了,这个方法就是几何法,没有什么比图形更容易让人理解了!
方法如下:
①构造一个边长为X的正方形,和一个长和宽分别是X和10的长方形,那么它们的面积之和便是X+10X;
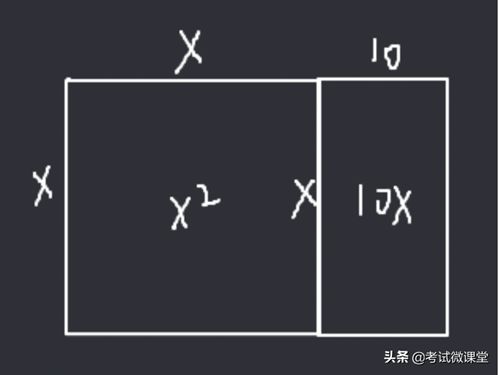
为了解X+10X=39这个方程,就是当图形面积是39的时候,边长X是多少?
②将矩形一分为二,也就是分成2个5X,然后将其中的一个5X平移到下方。此时的面积仍为39;
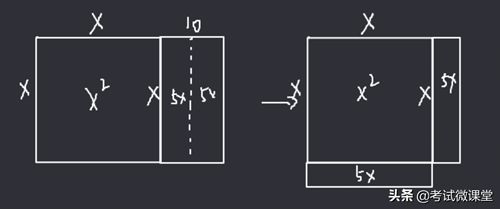
③将右下角缺失的正方形补全,容易知道虚线的小正方形边长为5,面积为25;
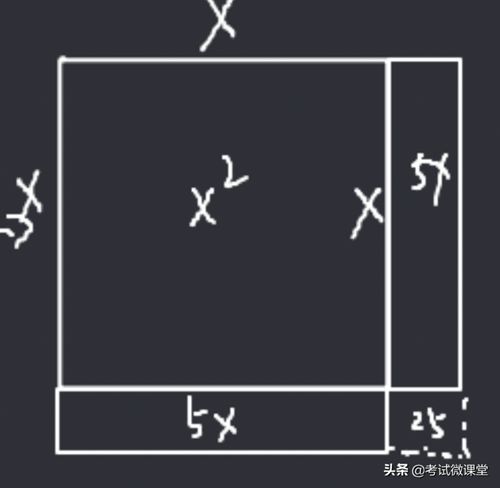
④此时大正方形的面积为39+25=64,那么大正方形的边长即为8,再将8减去5自然求得X=3。解毕!
可以看出在花剌子模的计算方法中,每一步都和他的几何证明严格对应,让人心服口服!花剌子模后,许多数学家也都在研究二次方程,从9世纪到16世纪,凡是关于代数的书几乎都是以“X+10X=39”这个为开始去讨论方程,如果二次方程界要拜祖师爷的话,那么花剌子模必定是第一人选!
中国古代的二次方程
我国历史上有很多杰出的数学家,比如祖冲之,秦九韶等大家都耳熟能详的名字,我们古代的数学重点在于“算”,可以说算学是异常的发达,经常令西方数学家瞠目结舌。既然要算,那么对于“二次方程”必然有所涉猎!对于中国的二次方程的解法,我们大致介绍两个时间节点的贡献,第一,《九章算术》,第二,《勾股圆方图》。
①《九章算术》卷九,中有一题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门一十四步折而西行一千七百七十五步见木,问邑方几何?答曰:二百五十步。”
翻译:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木,求小城的边长.
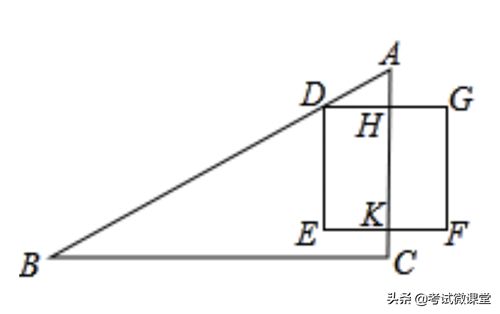
原文也给出了解法:“以出北门步数 20乘西行步数 1775倍之为实,并出南门步数 14为从法,开方除之,即邑方。”上文中的“实”指的是常数项,“从法”为一次项系数。从而可得二次方程:X+ 20+14X-2201775 = 0。至于这个方程是如何解出的,文中只有“开方除之”就把这个方程解决了,留给后人无限的遐想!当然这也非常符合《九章算术》的一贯作风,给个问题,配个答案,剩下的自己去想!后来刘徽在给《九章算术》作注的时候,也只是对为什么要如此列方程做出了合理的解释,至于如何解方程,依然是没有提及。
②公元3世纪的数学家赵爽在注《周髀算经》的时候,不仅给出了勾股定理的完美几何证明,同时也给出了二次方程的解法!其中的一段论文说:“其倍弦为广袤合,令勾、股见者自乘为其实。四实以减之,开其余所得为差,以差减合,半其余为广,减之于弦,即所求也。”
这里对抽象的文言不做过多解释,如果方程可以写成:X-bX+c=0的形式,则方程的根为X= b-√b-4c/2。可以看出,这几乎就是二次方程的求根公式,是二次项系数为1的时候。更厉害的,“其倍弦为广袤合”指的是两根的和为b,“令勾、股见者自乘为其实”指的是两根之积为c。说的就是根与系数的关系,完全是简配版的“韦达定理”,要知道这个结论可比韦达要早1300多年,所以也有人称赵爽为“中国的韦达”。
求根公式的发现
世界各地对二次方程的研究均有所涉及,那么我们所熟悉的二次方程求根公式是何时才问世的呢?说出来可能会吓您一跳,直到1768年,大数学家欧拉在《代数学入门》中给出了现在中学课本中的求根公式,这也是这个公式的首次问世。
虽然各路大神对二次方程都有独到的见解,但始终难有一个万能的公式去“一统江湖”,甚至在16世纪50年代,韦达已经提出了“韦达定理”,完美诠释了根与系数的关系,18世纪初,牛顿提出了二次方程的根与其判别式之间的关系。求根公式为什么却迟迟没有问世?
其实摆在数学界面前的有两座大山,一个负数,一个是虚数。几千年来,人们普遍不接受这两个“怪物”的存在,在计算中尽可能的去回避它们。比如负数,生活中真的看不见,摸不着,自然就不需要它们的存在。又比如虚数,那看起来更缥缈了,什么数的平方是-1?自然是没有的,本来负数就够牵强了,何况还要对它进行开方运算!问题就卡在了这里,如果接受了负数,就必须让负数拥有“合理的”开方运算,否则数学体系将不完备。人们一直在回避它们,然而它们又像幽灵一样,在计算中总是让人避之不及。
直到19世纪中期,数学家对代数方法的研究越来越完善,代数方程的研究演变成代数系统的研究,人们终于接受了负数和虚数,那么求根公式就应运而生!
以上就是(一元二次方程求根公式(一元二次方程求根公式是谁发明的))全部内容,收藏起来下次访问不迷路!