(惊了 我竟然在B站学)分部积分法之表格法

(惊了 我竟然在B站学)分部积分法之表格法

前言：关于分部积分法的文章，我实际上写的已经很多了，既有入门也有练习题，今天想跟大家分享的是分部积分法延伸出来的方法叫做表格法，这是张宇老师所讲的一种方法，像跟大家分享一下，可能以后再也不用∫udv=uv-∫vdu了，表格法用熟之后会更加简单

正文：

1.什么时候用分部积分法？基本公式推导过程

我们首先来回顾一下什么时候用分部积分法

①出现了不同类型函数乘积的时候

（反三角函数，对数函数，幂函数，三角函数，指数函数）

②求∫udv但求∫vdu简单的时候

公式推导过程如下

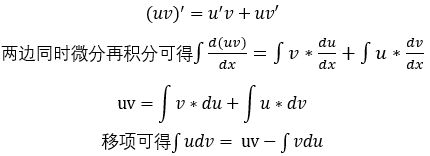
之前一片的文章有一个证明过程特别长的，两者结合着看吧效果更好有助于理解

2.选UV的三种情况，及推广式证明过程

在之前的学习过程中，肯定听说过一个口诀

反对幂指三or反对幂三指

现在来具体的分析一下这口诀

在这里说一下分部积分法的推广公式以及证明过程

事实上可以写成如下表格

黑色代表正号，红色代表负号，绿色最后具体情况具体分析

计算方法：以u作起点左上，右下错位相乘，各项符号“+”，“—”相间

最后一项为(-1)^n+1∫u^(n+1)vdx

接下来我会用几个例题来详细展示一般做法和表格法的区别

3.例题呈上

Ⅰ.

一般方法

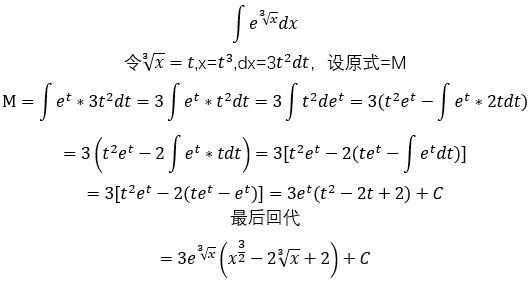
表格法

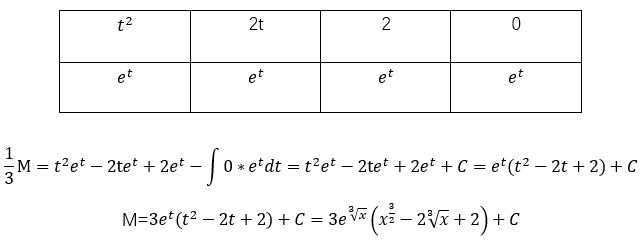
在这里肯定有老哥会说，这不是差不多嘛我用公式肯定比这个表格法快

那么我用下面这个例题来击毁你的围墙

Ⅱ.（情形一）

一般方法

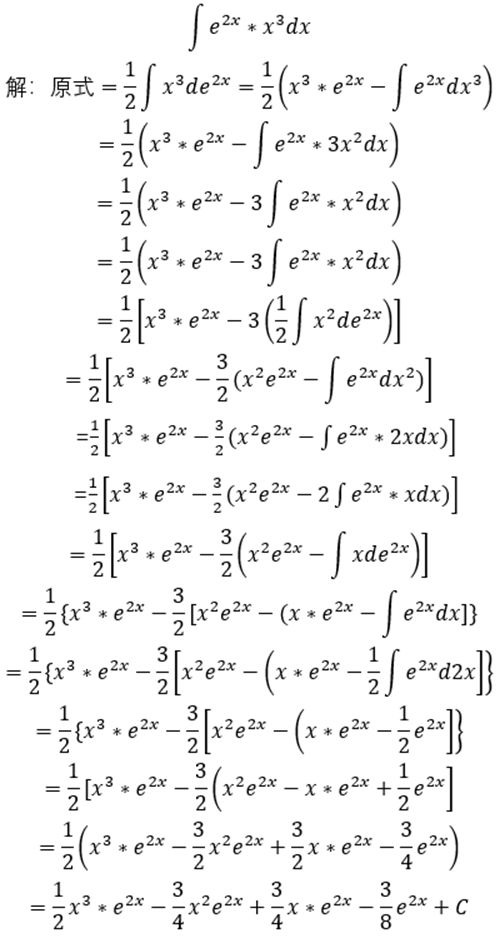
表格法

通过这个题目我们会看到表格法的优势，幂函数的次数越高，一般算法需要的步骤越多越容易出错，而表格法相对来说会越来越简单

Ⅲ.(情形二)

一般方法

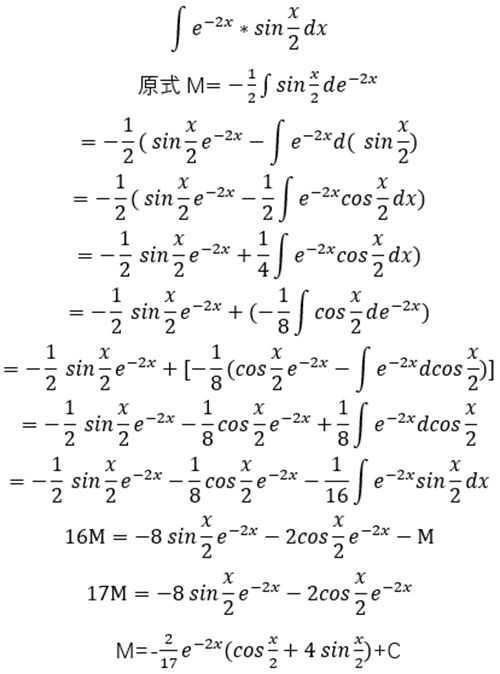
表格法

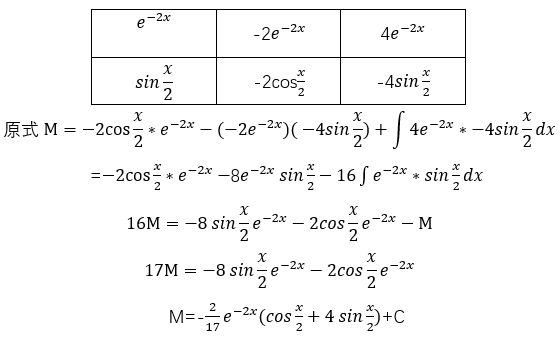
Ⅳ.(情形三)

一般方法

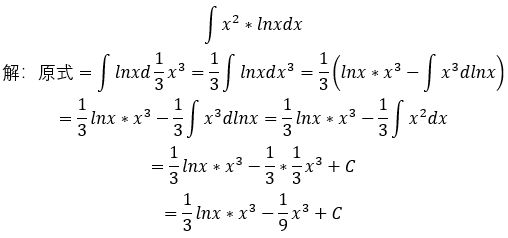
表格法

Ⅴ.(情形三)

一般方法

表格法

结语：

相信各位对表格法已经有了初步了解啦，希望以上的题能更好的帮助你理解表格法，在这里感谢张宇老师，部分文字来源于2021张宇基础30讲，UP主创作不易，整整花了3个半小时写了这篇文章，麻烦各位收藏打赏分享or点点广告吧，谢谢大家啦

对文章有什么疑问或错误，欢迎与我一起讨论

如果觉得文章还不错，点个打赏分享再走吧

笔耕不错，有你支持

（(惊了 我竟然在B站学)分部积分法之表格法）宝，都看到这里了你确定不收藏一下？？