正整数根的判别

正整数根的判别

已知正整数m满足m^2+5m+30是完全平方数，求m的值。

解：由题意得，设m^2+5m+30=n^2(n为正整数）

则得到关于m的一元二次含参方程m^2+5m+30-n^2=0

若方程有正整数解，则判别式Δ=25-4（30-n^2）=4n^2-95也应该为完全平方数。

令4n^2-95=a^2（a为非负数），则有（2n-a）（2n+a）=95.

又由于95只能分解成1*95或5*15两种情况，

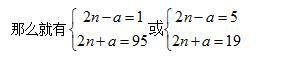
解得n=6或n=24

①当n=6时，m^2+5m+30=36，解得m=1或m=-6（舍去）；

②当n=24时，m^2+5m+30=576，解得m=21或m=-26（舍去）。

综上所述m的值为1或21.

一切真理源于猜想

（正整数根的判别）宝，都看到这里了你确定不收藏一下？？