隐函数求导公式,及运用

隐函数求导公式,及运用

隐函数求导公式是大学的一个知识，该公式在高中数学的“求圆锥曲线的切线方程”有重要运用 。 (这里只讨论一元隐函数的情况，因为多元隐函数的情况在高中数学的运用很少)

隐函数求导公式

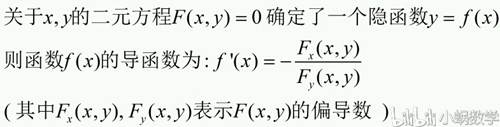
这个公式的好处是： 不用求出函数y=f(x)的具体表达式就能算出函数f(x)的导函数

下面举例说明该公式的运用

有人应该会问为什么不用x²+y²=r²解出y=f(x)的表达式，然后再求导，其实这种方法也可以，只不过要讨论两段函数，还要考虑正负的情况，有点麻烦，没有用隐函数求导公式方便

大家可以动一动手，仿造上述方法就可以得到如下结论

圆的切线方程的那个公式，大家应该很熟悉吧，当时我看资料书时，上面只写了公式，等上了大学后，学习了《数学分析》后再来回顾高中的数学知识和题目时，才发现原来是利用隐函数求导公式就能快速地算出圆锥曲线上某一点切线的斜率，从而计算出圆锥曲线上某一点的切线方程。(其实利用圆锥曲线的方程解出函数的具体表达式，然后再求导也可以计算，只不过要分情况讨论，还要考虑正负号的情况，计算过程一点麻烦)。圆，椭圆，双曲线，抛物线的切线方程，大家可以记忆一下，可以提高自己的解题速度。

（隐函数求导公式,及运用）宝，都看到这里了你确定不收藏一下？？