高数近期优秀题目汇总(2.2~2.4)
高数近期优秀题目汇总(2.2~2.4)
前言:近期的好题目有点多,或者说不会的题目有点多,有些是我本来就会的但我觉得蛮重要,有些是我不会的觉得题目蛮好的就分享给大家啦,希望做一个题,总结一种做题思路吧,毕竟题目做不完的,方法就那几种,万变不离其宗
正文:
1.
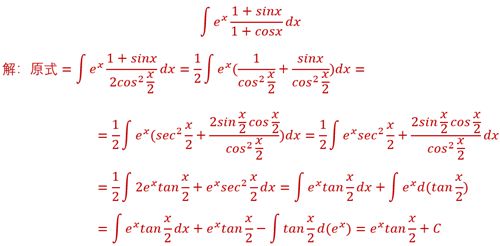
说实在的,这题目我一上来都傻了,根本无从下手啊,直到问了大佬之后,给了一点铺垫我才解出来,这辈子应该不会忘了这个题了,主要用的是分母如何处理,对于分母的处理是解这个题目的关键,还有一种方法更加巧妙,我放在下面
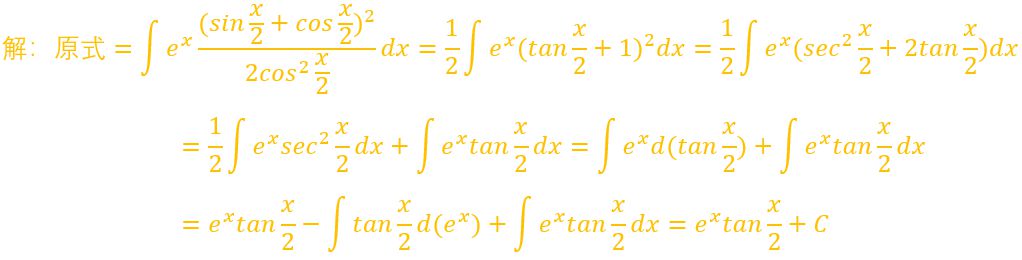
后者的方法巧妙之处在于对分子的处理上,个人觉得比上一个方法更加简练,这个题目可真是给我留下了不可磨灭的印象(sin²x+cos²x=1)
2.
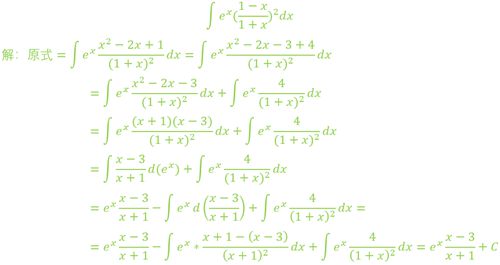
对于这个题目而言,重点是对分子的处理上,如何消掉分母的二次方,很巧的是再算最后的时候分母的二次项跟前者正好互为相反数相消,无巧不成书鸭
这个题目的来源,有一段小插曲,是凭空出来的一道题目
原因是我在写第三题的时候抄错题了,但结果算对了,看看下图我哪里写错啦,哈哈(粗心)
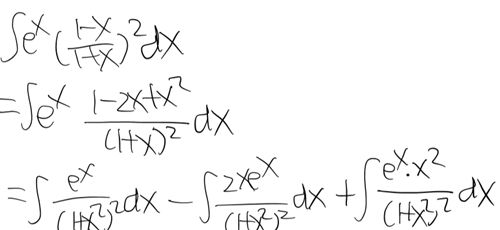
造成这一现象的原因是估计没看手抄的题目,看的是发的图片解的题目吧,你会发现第二题和第三题是姊妹题,看看哪里有不同哦
3.
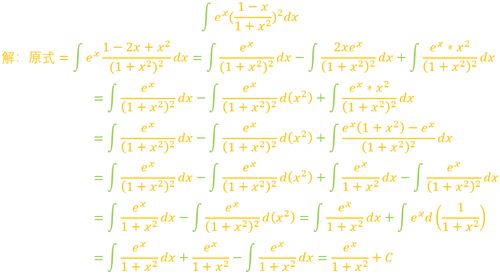
第三道题虽然只跟第二题分母差了个平方,但解题的风格却大相径庭,跟像是好几个不定积分题目的组合体,又是无巧不成书不定积分项全消了,好好对比这两个题目,或许给你一些新的启发
4.
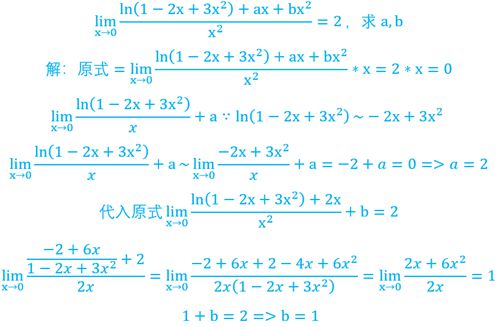
经典的求极限未知数问题,这也应该算求极限的一大类题型了,当然也可以用泰勒公式来求解,这次我用的洛必达法则,洛必达天下第二,泰勒天下第一哈哈哈
5.
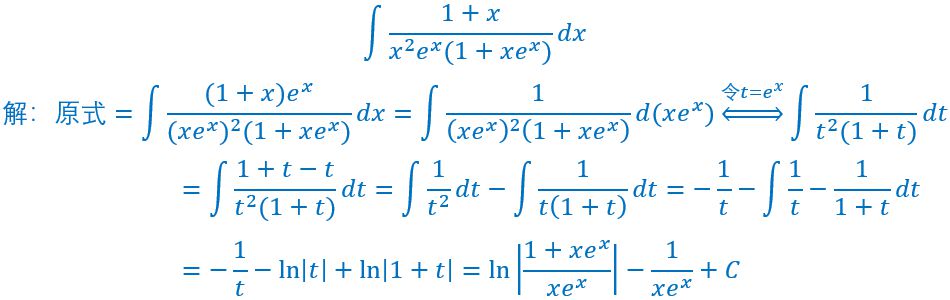
这个题目的难点在于很难凑,x*e^x是这个题目的关键,如果你想不起来换元或者它的导数公式,那就很难解出来了
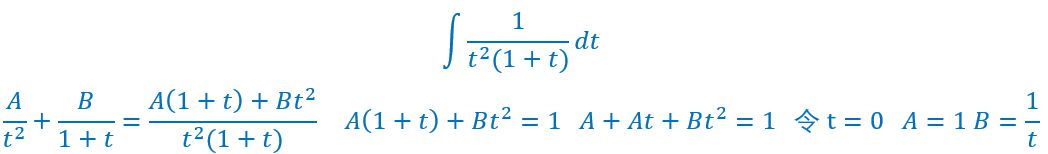
当然遇到分母两项之积,如何拆成独立的两项是一个重要的问题,思路有两种,第一种是凑跟分母相同的项目然后相消,第二种就是我上面的那个图片待定系数法,如果这种方法不会的建议食用有理函数积分的完整方法这篇文章
6.
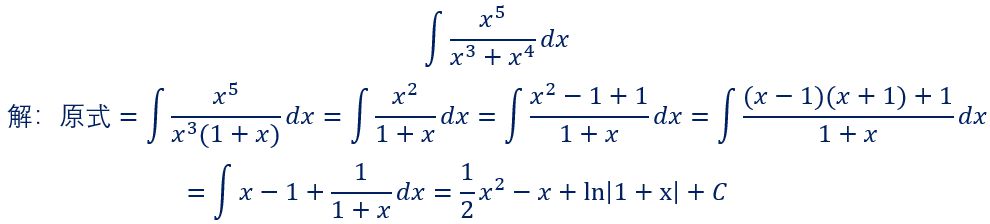
看到分子分母有相同的因子,一定要第一时间先化简相消,再用平方差公式拆开,难倒不难,怕的是一上来先被他的外表所吓倒
7.
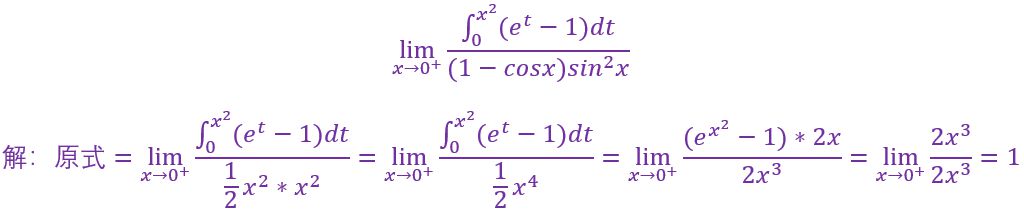
变限积分函数求极限,一定要用洛必达法则
变限积分函数求极限,一定要用洛必达法则
变限积分函数求极限,一定要用洛必达法则
8.

这个题第一眼应该不会让你会想到三角代换
但是分母的特点不就是arctanx的导数么?对吧
换元必换限,还用到了区间再现公式以及高中的基本三角公式
看起来简单,做起来水平蛮高的一道题,好好做做吧

对文章有什么疑问或错误,欢迎与我一起讨论
如果觉得文章还不错,点个打赏分享再走吧
笔耕不辍,有你支持

(高数近期优秀题目汇总(2.2~2.4))宝,都看到这里了你确定不收藏一下??