辅助角公式

辅助角公式

辅助角公式：

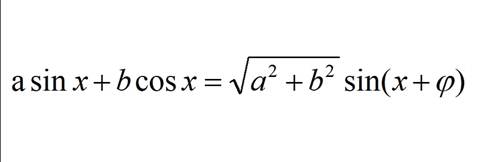
，其中tanφ=b/a（a0）.

该公式的主要作用是将多个三角函数的和化成单个函数，以此来求解有关的最值问题、周期问题等。

1、推导过程

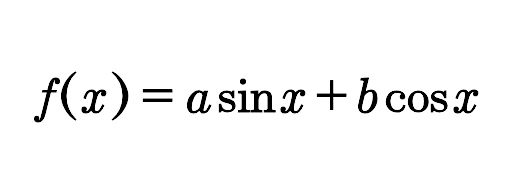
变形得

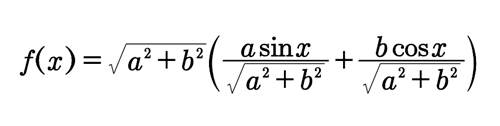
为利用两角和差公式化简，设-π/2φπ/2

令

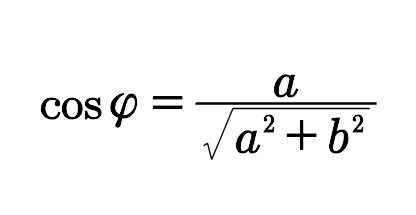
（注意到a0）

则

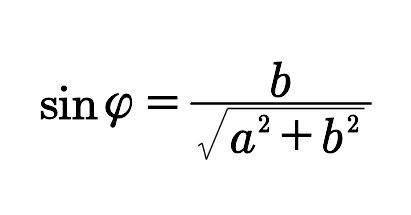
其等价于tanφ=b/a

则

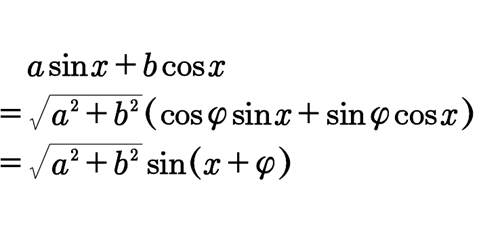
即

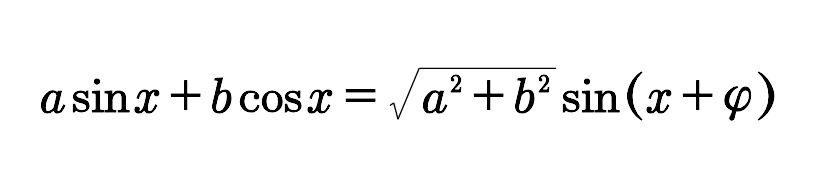
其中tanφ=b/a

若令

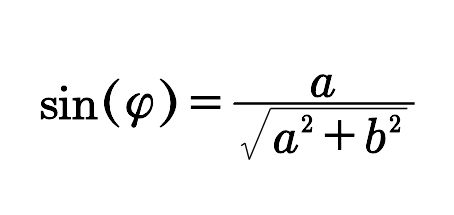
则

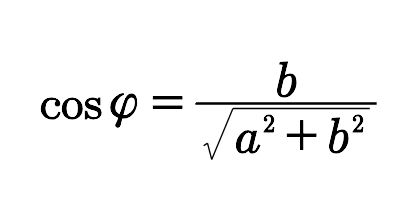
（b0）

其等价于tanφ=a/b

则

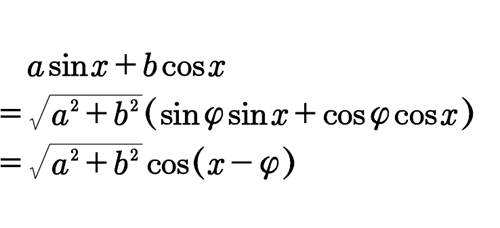
即

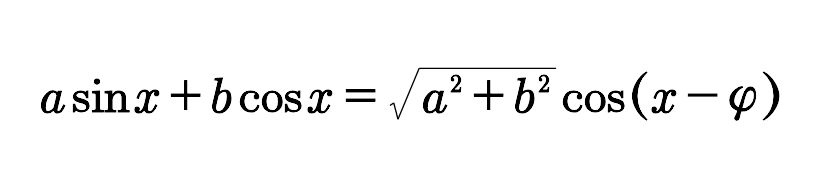
其中tanφ=a/b

注意：两种令法中初相用了同一个字符φ表示，但含义不同，要区分。

2、分析意义

我们需要分析公式中每一个量的意义。

先看等式左边是两个分别增大（或减小）一定倍数的正弦与余弦函数的和。

再看等式右边是一个增大（或减小）一定倍数并且被改变了初相的正弦函数。

从代数意义上讲，辅助角公式是为了将几个同频率的正弦型函数求和，转化为一个单独的正弦型函数而诞生的。频率相同意味着ω相同，所以对于辅助角公式而言，为了方便起见，我们只讨论ω=1时的特殊情况。在这种情况下，对于一个正弦型函数，我们只有A（增大的倍数）与φ（初相） 两个量需要讨论。

我们可以把A看作大小，把φ看作角度。而角度和大小恰是极坐标系确定位置的两个要素。

辅助角公式与极坐标系有什么关系吗？

简化验证

简化问题，使a=b=1，得

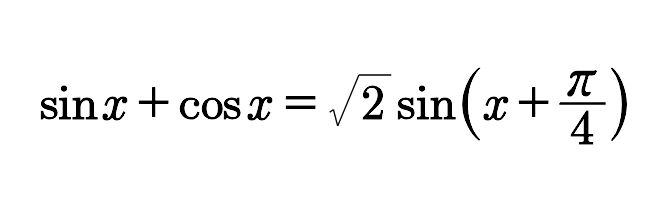
又∵

∴

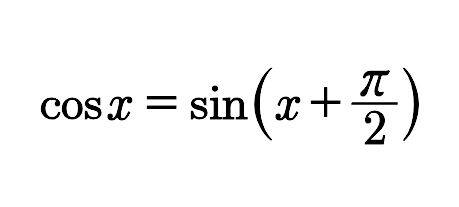
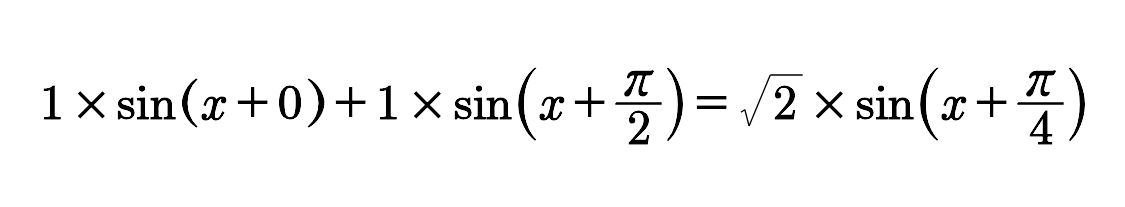
而在极坐标系中平面向量的加即为

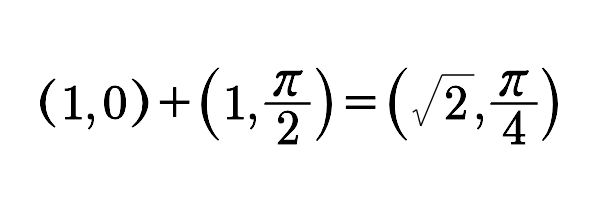
（如下图）

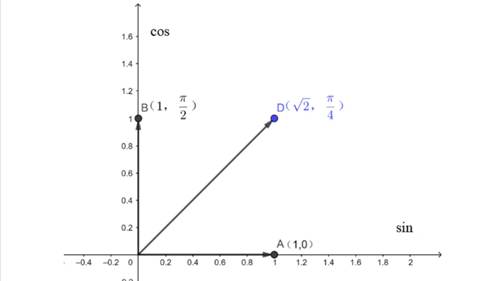
两者之间有异曲同工之妙。

即sin与cos都只是单位向量，

而a、b两者是单位向量的变化幅度，

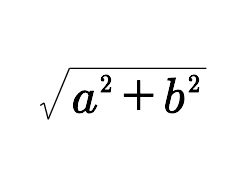
是两向量和的模，φ则是和向量与横轴的夹角。

推广延伸

之前的验证只是在a=b=1下进行的。其实，这一结果具有普适性。

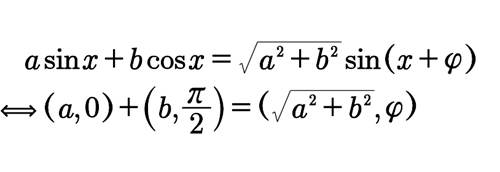
注：这种几何意义同样适合推导诱导公式等部分三角函数恒等变换公式，但三角函数间乘法不等价于单位向量间点乘（即数量积）。

3、疑问

为什么在推导辅助角公式的时候要令辅助角的取值范围为(-π/2,π/2)？其实是在分类讨论a0或b0的时候，已经把辅助角的终边限定在一、四象限内了，此时辅助角的范围是(2kπ-π/2,2kπ+π/2)(k∈Z)。而根据三角函数的周期性可知加上2kπ后函数值不变，况且在(-π/2,π/2)内辅助角可以利用反正切表示，使得公式更加简洁明了。

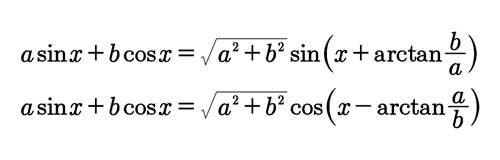
个人推荐第一种书写形式，等式左边读时，先读a再读到b，右边读到分数时先读分母再读分子，也是先读a再读到b，而且有三个加号，这样记忆不易出错。

当然本文开头的书写形式也推荐，把一个长式子分两段来记，减少了记忆难度，其次若忘记了φ等于多少，还可以根据第一段公式逆推。

最后将公式汇总如下

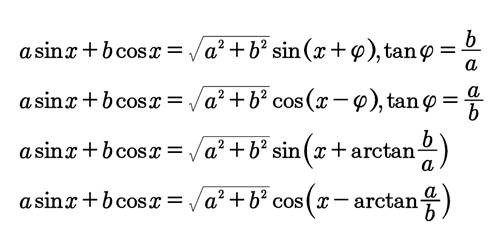
4、提出者

李善兰

李善兰，出生于1811年 1月22日，逝世于1882年12月9日，浙江海宁人，是中国近代著名的数学、天文学、力学和植物学家，创立了二次平方根的幂级数展开式，研究各种三角函数，反三角函数和对数函数的幂级数展开式（现称“自然数幂求和公式”），这是李善兰也是19世纪中国数学界最重大的成就。

（辅助角公式）宝，都看到这里了你确定不收藏一下？？