第一类换元积分法

第一类换元积分法

正文：

1.什么是第一类换元积分法？

我先把定义放在这里以供参考

如果上面的图片看不懂？那你肯定知道凑微分这个名词吧

它实际上是复合函数求导法则的逆过程，其关键是“凑微分”，

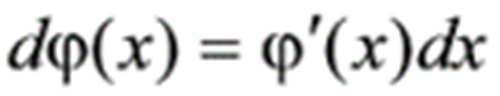
如果复合函数求导没搞清的，我之前写过关于复合函数求导的文章

链接在此：复合函数求导与基本初等函数（点击文字即可进入）

2.基础例题呈上

我在这先提一句，这一句话非常重要，本段话来自于张宇《高等数学18讲》

最好写在笔记本上，因为我从没见到过文字能够如此清晰表述凑微分的过程

例一

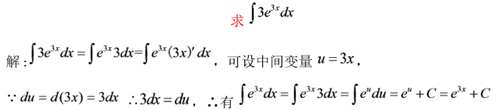
首先观察被积函数的复合函数是什么样的，其次看是否有它的内函数的导数

若没有就去凑成想要的形式

例二

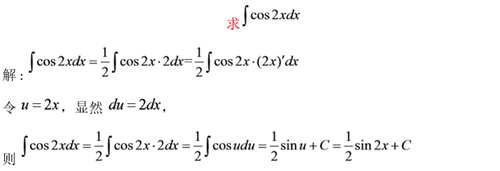
在比较熟练后，我们可以将设中间变量的过程省略，从而使运算更加简洁

例三

如果碰到3次及以上的更高次数不要急着去拆分，试着去凑微分会更好

例四

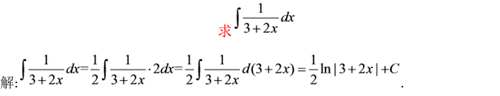
凡是属于第一类积分的题，都不能直接用基本积分公式，需要凑微分换元

例五

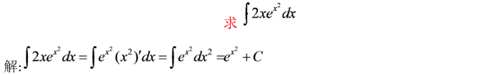
还是那句话，要想学好积分，得先学好微分

例六

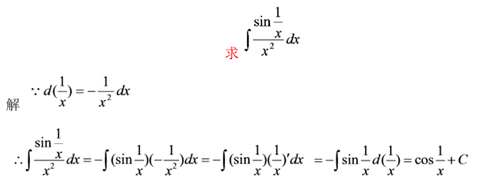
这个题属于基础题的范畴，基本上一眼就能看出来需要凑哪一项

3.加油站

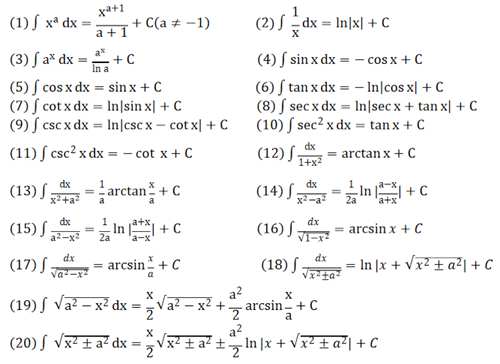
还是那句话，如果前十六个基本积分公式都背不下来，那甭做题了，做一个卡一个

有些积分公式难记不好推导的我也写过文章

链接在此：旧文新发--不定积分公式推导 （点击文字即可进入）

对于后四个公式，对于专接本而言，能记就记不强求

但对于考研而言，不仅要记住，更重要的是推导过程，以及思维的建立

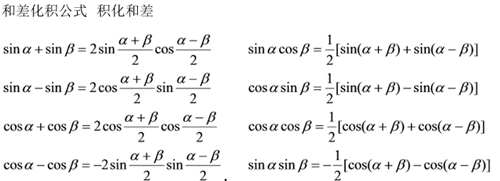
考研党必须记住以上八个公式

4.综合例题呈上

例七

本题就用到了三角函数的降幂公式

例八

分母提出一个a²，然后换元套用基本积分公式求得即可

例九

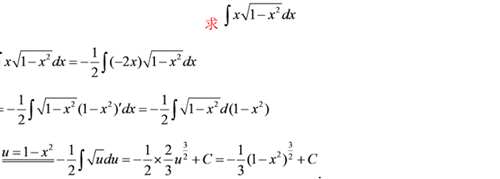
本题达到了凑微分题难度的平均水平了，之前的例题都还基础

例十

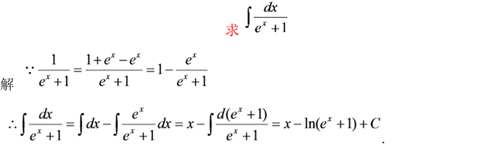
解这个题就需要一定的技巧了，常说的+n-n这个技巧在这里就表现得淋漓尽致

在这里n就不单单表示整数了，函数也可以

例十一

本题技巧就是分子分母同时除以4^x次方，遇到这种情况，一般是除以底数较小的项

例十二

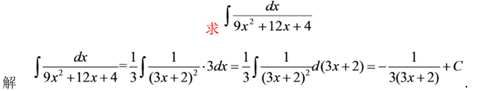
这个题难度有点高，容易一下子让人摸不到头脑

遇到凑不了，不知道该怎么凑的情况，要想之前初高中所学的基本数学公式

例如平方立方差公式，完全平方立方公式

和差化积，积化和差诸如此类公式

例十三

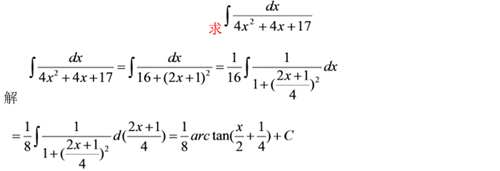
被积函数分母是二次三项式且不可以分解因式，不是完全平方式时可以把分母配方化为的形式

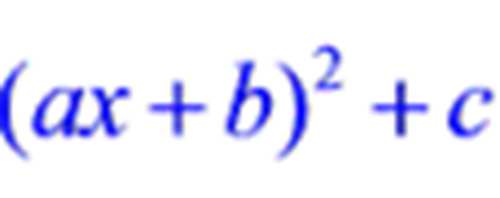
，然后利用

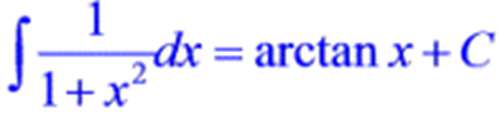
来求解

例十四

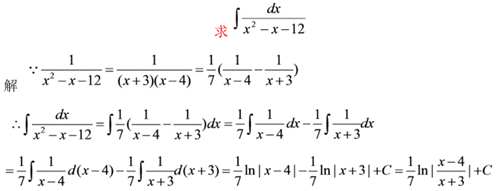
分子是常数，被积函数分母是二次三项式且可以分解因式

被积函数可以用裂项法转化为两个简单分式的差

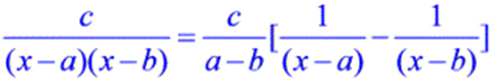
例十五

被积函数分子是一次多项式，分母是二次多项式时，首先把分子凑成分母的导数

例十六

本题如果没记住积化和差公式，那就很难说了，几乎无解

3.归纳总结

1 . 第一换元法是把被积函数 g ( x ) 凑成

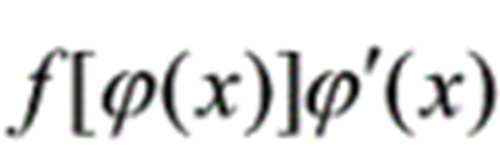
的形式然后应用公式

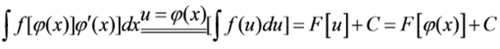
2. 要熟练掌握几种典型的“凑微分”的方法。

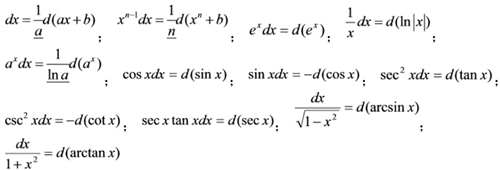
3. 熟练掌握几种典型用第一换元积分法计算的不定积分

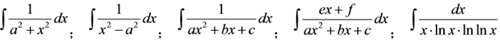
4.结语

各位看在我这么用心的份上，麻烦多多转发分享，如果能打个赏那就更好了

下面是本文章所用到的图片，本文章1326字

*本文章素材来源于

对文章有什么疑问或错误，欢迎与我一起讨论

如果觉得文章还不错，点个打赏分享再走吧

笔耕不错，有你支持

（第一类换元积分法）宝，都看到这里了你确定不收藏一下？？