高等数学-导数的定义以及简单的求导

高等数学-导数的定义以及简单的求导

人们最初研究导数是从各种物理现象开始的，现在我们就先扯扯物理吧o(*￣▽￣*)o

我们都知道这个公式：

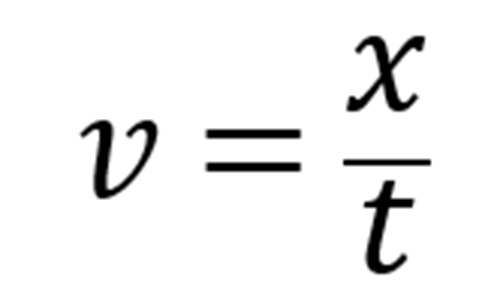
x表示位移，t表示时间

这个公式又和导数有什么关系？我们从研究瞬时速度的表达式说起

学过高中物理的人都知道，在x-t坐标轴中，斜率表示速度对吧？（废话啊(o|o) ）

那么，对于x-t坐标轴而言，有

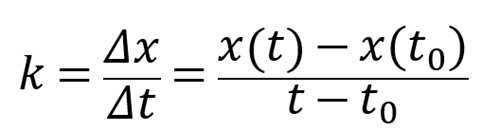
k表示在x-t坐标轴的斜率，它表示速度; x(t)表示一个位移函数

其实也就是

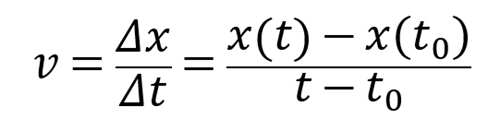
我们不是要求瞬时速度喵？现在该怎么办？

莫急~就快了

你有没有发现，当Δt-0的时候，v就是瞬时速度了？没有？听我细讲~

当时间间隔越来越小，不就越接近于瞬时了？

因为

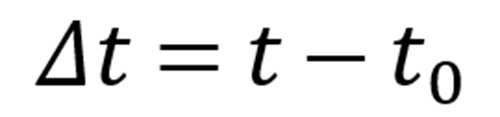
且

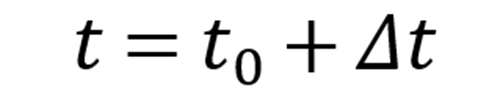
代入，得到

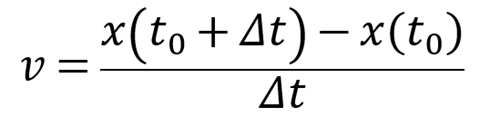
这个式子样子已经接近于导数的定义式了，但是我们要求的是瞬时速度

所以这个时候该怎么？

当然是极限啦！极限大法好极限大法好d=====(￣▽￣*)b

因为有

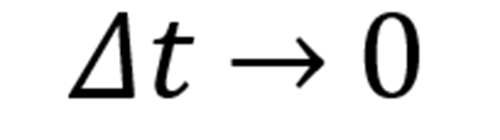
所以取极限，我们就得到

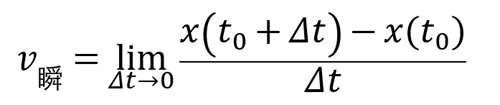
这就是瞬时速度的表达式了，其实这也是导数的定义式（不太正式而已hhh）。

第二节 导数的定义与公式

一、定义

由于专栏不支持公式编写，所以我用word打了一遍

导数的定义（改编自度娘百科）

特别的

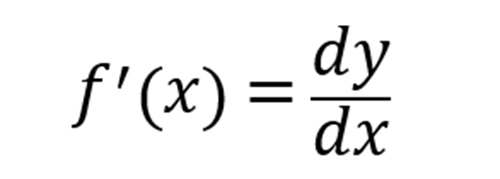
微分

dy和dx是微分，求导过程也就是微分过程（我们以后见到更多的是微分形式！或许是不用写极限这个臭长的式子才流行的吧...）

有人说，导数的本质是什么。其实这也不太好解释，毕竟有好多方面解释导数呢。这里我就简单说说：

导数本质是瞬时变化率，就是Δy/Δx的比值（有人估计到这里还是不太懂）

直白的说，设函数g(x)=kx，根据本质是瞬时变化率，而一次函数的变化率保持不变，那么g(x)=k.

可以说，在线性函数中，导数就是斜率。

如果在曲线函数，那么导数就是切线斜率，这个我会在后面解释

二、公式

这里我就不给证明过程了，太长了（各大教科书都有证明过程的）

为了方便（偷懒），在这里我们用f(x)=d(f(x))/dx表示

第三节 求导

在这里，我尽量选择较简单的题（以基础为重）

例题1：已知函数f(x)=x^3+2x^2+3，求dy/dx

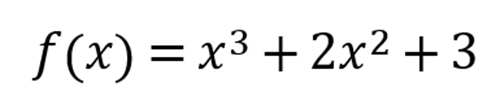
在这里主要是想让读者先熟悉微分形式

很明显，这个是让你求导的题

我们将使用定义来求导：

首先，取极限

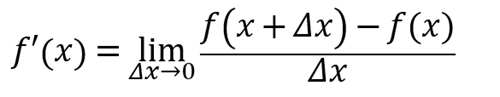
代入f(x+Δx)和f(x)，得

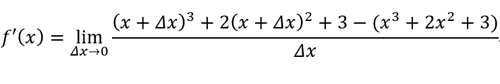
展开，得到

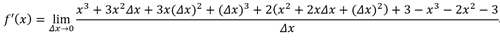
woc这么长

化简，我们就得到了

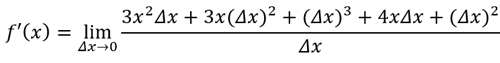
约分，得到

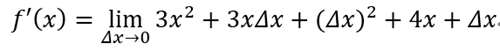
现在就简单了，我们直接使用代入法，最终得到

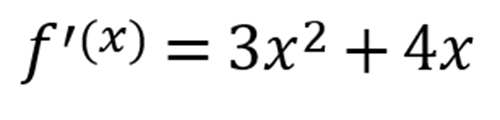
即

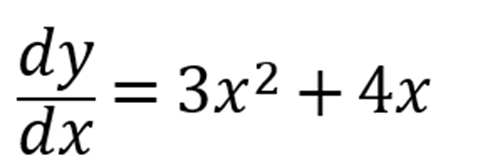
到了这里，我们得到了一个结论，这个结论会使你的解题速度加快：

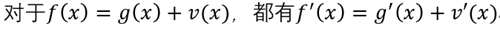
我把这个结论称为分别求导原则（只有加减的时候有效）

比如f(x)=x^2+5x

那么f(x)=2x+5

只要你掌握了公式，这题瞬间就成了口算题

例题2：已知函数f(x)=(x^2+2x)(x^3+2x)，求f(x)

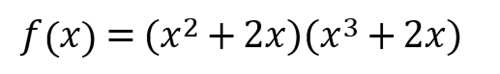
很明显，这里考察的是导数的乘积法则，我们令

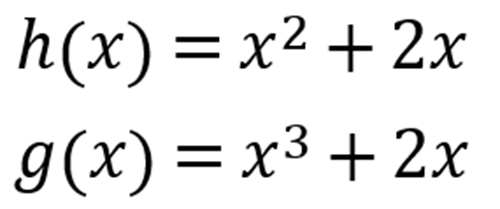
那么

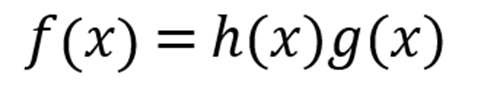
使用公式

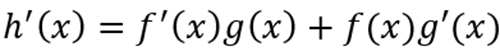
即

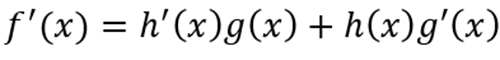
又因为

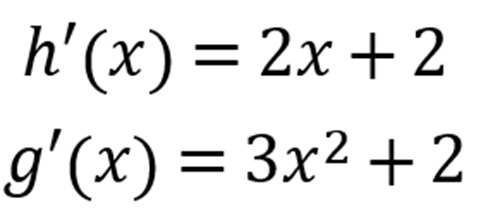
代入公式，得到：

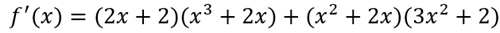
多项式展开，得到

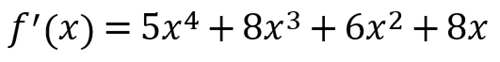
这就是答案了

例题3：已知函数f(x)=(2x^3-3x+1)/(x^5-8x^3+2)，求dy/dx

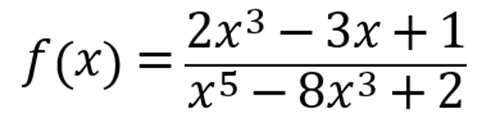
这里考察的是商法则的运用

这次我们试试如何用微分形式求导

令y=f(x), u=2x^3-3x+1 , v=x^5-8x^3+2

则

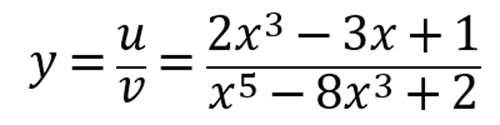
根据商法则的微分形式

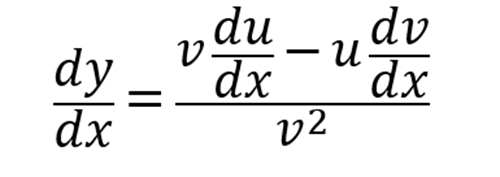
其中

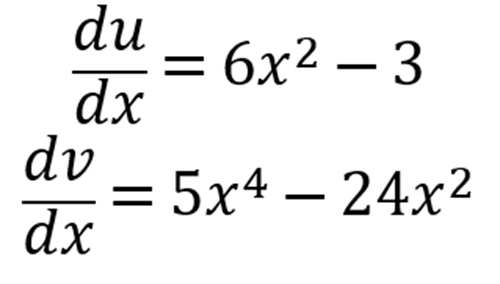
到这里，估计有人就看不懂了，这个du/dx究竟是什么东西？！

很简单，就是u对x求导（可以类比dy/dx）的意思。也就是u是一个新的函数，自变量仍然是x，而du/dx就是u函数的导数。

代入就得到

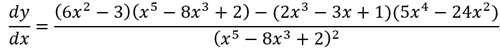
以上就是（高等数学-导数的定义以及简单的求导）全部内容，收藏起来下次访问不迷路！