(五分钟机器学习)决策树模型中的CART算法

(五分钟机器学习)决策树模型中的CART算法

哈喽大家好！我是爱讲故事的某某某， 欢迎来到今天的5分钟机器学习专栏---CART决策树

今天我们继续视频的内容来讨论如何用另一个方法去训练决策树模型，也就是Classificaion And Regression Tree (CART).

还没有看过的小伙伴们欢迎去补番这个视频：

这种方法是一种很重要的方法，之前我们讲到的ID3模型只适用于训练一个决策分类树，也就是说如果你想做一个Regression Task（比如预测一个产品未来的价格），ID3是做不到的。

但是我们现在讨论的CART方法，既可以用于训练一个决策分类树，也可以训练一个决策回归树。它是一种二分递归分割技术，把当前样本划分为两个子样本，使得生成的每个非叶子结点都有两个分支（如下图）：

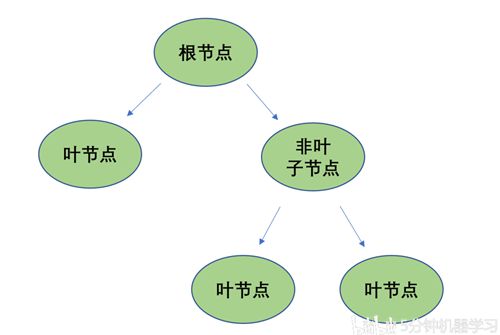
Fig1. 二叉树的基本结构

因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树，它在每一步的决策时只能是“是”或者“否”，即使一个feature有多个取值，也是把数据分为两部分。这点其实和我们之前讲到的ID3不同，ID3在每一个子节点是可以分成3个以上叶节点的。

在CART算法中主要分为3个步骤，这点和我们在视频中学到的ID3很像：

Step 1: 从根节点开始，每一个节点中我们便利所有可能的Spliting Criteria，也就是决策条件

Step 2: 验证决策条件，并进行剪枝

Step 3: 重复Step 1 Step 2，直到达到最大树的深度，或者所有叶节点中的数据属于同一类。

但是，和ID3不同的是，CART 方法不再使用信息增益论作为决策条件的评估方法。相似的，他会采用一种叫做Gini Index（也叫Gini指标）的方法去评估每个决策条件。这个方法是用来衡量频率分布值的状况。他的取值在0~1之间，当Gini = 1，意味着当前节点内的分布极度不平均（全部不一样）；反之，当Gini = 0, 意味着当前节点内的分布绝对平均（都一样）。

我们用Gini的计算结果去评估一个决策条件的好与坏，也就是说，我们希望Gini越小越好（Gini越小，意味着采用当前决策条件所产生节点里的样本同质度更高）。他的计算公式如下：

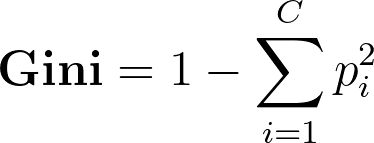
Fig2. Gini index计算公式

在这个式子中，C表示样本的类别数，而pi表示第i类样本在当前节点内的概率。有了这个公式，我们就可以评估每个决策条件，从而找到最适合于当前节点的了。

好了，以上就是今天的内容了。在本文的最后，给你一个小测验。

基于下面图中的数据(第一列Customer 为序列，第二列Income 到第四列 Marital Status为我们的属性列，最后一列Purchase为输出列，即类别信息)，采取Gini Index评估的话，我们应该选下面哪个决策条件呢？

A: Income = Low

B: Education = Univeristy

C: Marital Status = Single

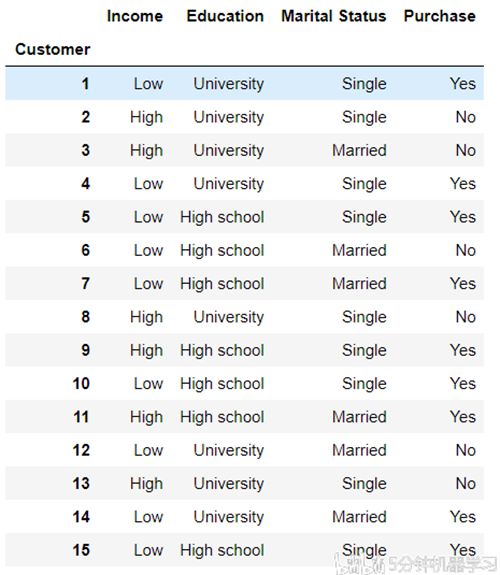
Fig3. Purchases Age dataset 

（(五分钟机器学习)决策树模型中的CART算法）宝，都看到这里了你确定不收藏一下？？