梯度 方向导数 散度与旋度

梯度 方向导数 散度与旋度

1.梯度gradient：

向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

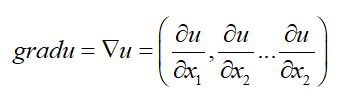
梯度表达式（式1）

2.方向导数

在函数定义域的内点，对某一方向求导得到的导数，

n向量为某一方向向量

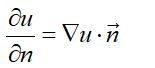
方向导数表达式（式2）

3.散度

标量，散度可用于表征空间各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。

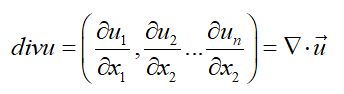
散度表达式（式3）

4.旋度

向量,无旋场就是有势场；表示三维向量场对某一点附近的微元造成的旋转程度。

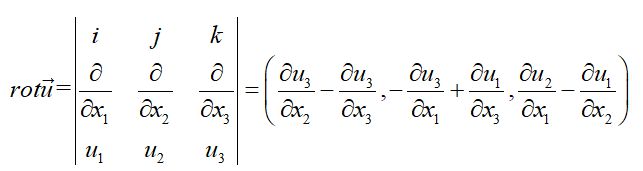
旋度表达式（式4）

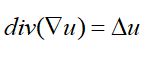
散度（梯度u）=拉普拉斯u（式5）

散度定理

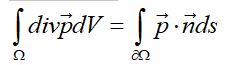
一个向量p的散度在区域的积分=向量与该区域外法线方向的点积在边界的线积分（式6）

若取向量p为梯度u,即可得格林公式的特殊形式

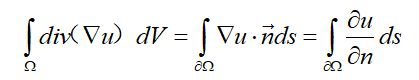
（式7）

格林第一公式：

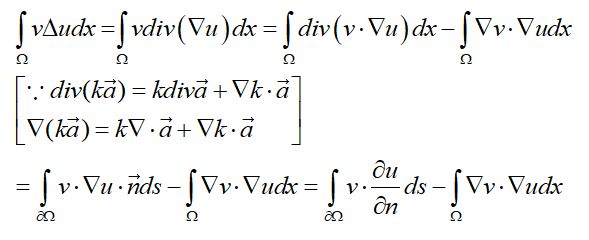
略去对u，v的要求的格林第一公式（式8）

同理：

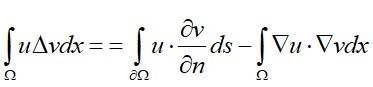
（式9）

上述两式相减得格林第二公式：

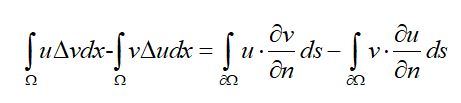
（式10）

特别的：

取v=1：得式7

对格林第一公式，取拉普拉斯u=0：

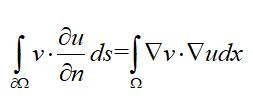
（式11）

对格林第二公式，取拉普拉斯u=拉普拉斯v=0:

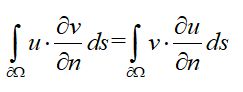
（式12）

（梯度 方向导数 散度与旋度）宝，都看到这里了你确定不收藏一下？？