虚数及其运算定律

虚数及其运算定律

在数学中，虚数就是形如a+bi的数，其中a,b是实数（整数、分数、无理数），且b≠0,i² = - 1即i=√-1（若a^2=b,则a=√b）。后来发现虚数a+bi的实部a可对应平面上的横轴，虚部b与对应平面上的纵轴，这样虚数a+bi可与平面内的点(a,b)对应。

直角坐标系

可以将纯虚数bi添加实数a以形成形如a + bi的复数，其中实数a和bi分别被称为复数的实部和虚部。

三角函数

sin(a+bi)=sin(a)cos(bi)+sin(bi)cos(a)

=sin(a)cosh(b)+isinh(b)cos(a)

cos(a-bi)=cos(a)cos(bi)+sin(bi)sin(a)

=cos(a)cosh(b)+isinh(b)sin(a)

tan(a+bi)=sin(a+bi)/cos(a+bi)

cot(a+bi)=cos(a+bi)/sin(a+bi)

sec(a+bi)=1/cos(a+bi)

csc(a+bi)=1/sin(a+bi)

四则运算

(a+bi)±(c+di)=(a±c)+(b±d)i

(a+bi)(c+di）=(ac-bd)+(ad+bc)i

(a+bi)/(c+di)=(ac+bd)/(c²+d²)+(bc-ad)i/(c²+d²)

r1(isina+cosa)r2(isinb+cosb)=r1r2[cos(a+b)+isin(a+b)]

r1(isina+cosa）/r2(isinb+cosb)=r1/r2[cos(a-b)+isin(a-b)]

r(isina+cosa)n=r^n(isinna+cosna)

共轭复数

a+bi=a-bi

-(z1+z2)=_z1+_z2

-(z1-z2)=_z1-_z2

-(z1z2)=_z1_z2

-(zn)=(_z)n

-z1/z2=_z1/_z2

-zz=|z|²∈R

乘方

zm·zn=zm+n

zm/zn=zm-n

(zm)n=zmn

z1m·z2m=(z1z2)m

(zm)1/n=zm/n

z·z·z…·z（n个）=zn

z1n=z2--z1=z21/n

ln(a+bi)=ln(a^2+b^2)/2+i Arctan(b/a)

logai(x)=ln(x)/[ iπ/2+ lna]

xai+b=xai·xb=eialn(x)·xb=xb[cos(alnx) + i sin(alnx). ]

在数学里，将偶指数幂是负数的数定义为纯虚数[若a^2n(n∈N)=-b(b∈R,b0),则说a为纯虚数]。所有的虚数都是复数。定义为i²=-1。但是虚数是没有算术根这一说的，所以±√(-1)=±i。对于z=a+bi,也可以表示为e的iA次方的形式，其中e是常数，i为虚数单位，A为虚数的幅角，即可表示为z=cosA+isinA。实数和虚数组成的一对数在复数范围内看成一个数，起名为复数。虚数没有正负可言。不是实数的复数，即使是纯虚数，也不能比较大小。

我们可以在平面直角坐标系中画出虚数系统。如果利用横轴表示全体实数，那么纵轴即可表示虚数。整个平面上每一点对应着一个复数，称为复平面。横轴和纵轴也改称为实轴和虚轴。在此时，一点P坐标为P （a，bi），将坐标乘上i即点绕圆心逆时针旋转90度。

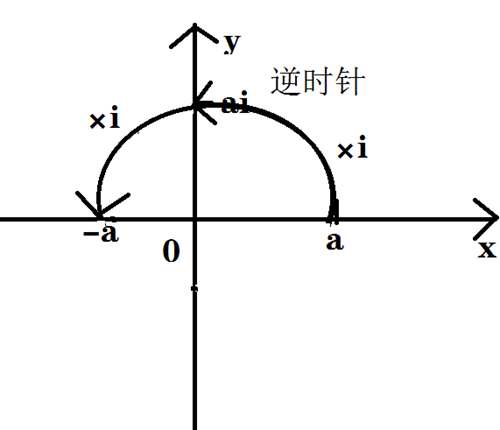
之所以转了两次之后a变成了-a，是因为aii=(-1)a=-a；所以“将坐标乘上i即点绕圆心逆时针旋转90度”成立

一个数的ni次方为：

x^ni = cos(ln(xn)) + i sin(ln(xn))

若x=e,n=π，则x^ni =e^iπ=-1,两边各加1，得欧拉公式：e^iπ+1=0

一个数的ni次方根为：

ni√x= cos(ln(x1/n)) - i sin(ln((x1/n))

以i为底的对数为：

log_i(x) = 2 ln(x)/ iπ

i的余弦是一个实数：

cos(i) = cosh(1) = (e + 1/e)/2 = (e² + 1) /2e = 1.54308064

i的正弦是虚数：

sin(i) = sinh(1) i =[(e - 1/e)/ 2]i = 1.17520119 i

以上就是（虚数及其运算定律）全部内容，收藏起来下次访问不迷路！