零点分段法
零点分段法
本文章适用于初一学生
|x+5|这是一个绝对值,很简单对吧
但是我们要如何化简它呢?
我们大家都知道,绝对值表示的是一个数在数轴上距离零点的距离,也就是说无论什么数加一个绝对值都是正的
那么,当里面的数值是负数时,我们就应该把里面的东西加一个负号,把它变成正的,就可以化简了
即当x+50,即x-5时,原式可化简为-(x+5)=-x-5
当x+5大于0时,里面的东西就不用动了,化简为x+5
当x+5=0时,那自然就化简成0(((
那么我们接下来看点难的
|x+5|+|x-5|该怎么化简?
我们首先看到,第一个式子在x+50时不用动,在x+50时变成负的
因此,我们把这中间的x+5=0叫做“零点”,即x=-5
第二个式子的零点是x-5=0,即x=5
那么我们在数轴上把这两个点画出来
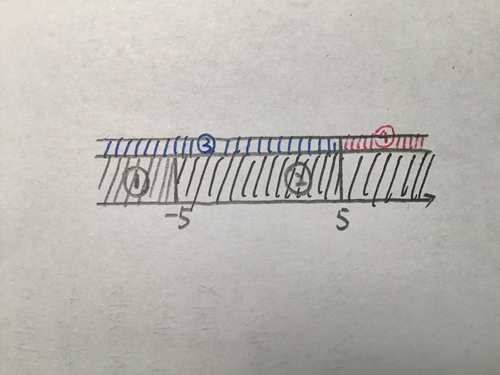
x-5时,第一个式子化简为-x-5
x-5时,第一个式子化简为x+5
x5时,第二个式子化简为-x+5
x5时,第二个式子化简为x+5
那么,大家可以看到中间的2和3部分有重叠
因此我们把它分成三个部分!
x-5时,原式化简为(-x-5)+(-x+5)=-2x
-5x5时,原式化简为(x+5)+(-x+5)=10
x5时,原式化简为(x+5)+(x-5)=2x
还有两个零点处,可以随便分到相邻的哪一部分,我一般是喜欢都分到中间的第二部分去,那两个小于号就都变成小于等于。
就这样我们就把这个绝对值式子化简啦
这个非常重要,因为初一学生的数学考试第24题压轴就是所谓“数轴动点”,必须要用到这个绝对值化简的零点分段法,因此大家要非常熟练!!!
来布置课后作业,要记得零点分段!
|x-6|
|x-4|+|x-3|
|x-8|-|x+10|
|x+1|+|x+3|+|x+5|(提示:本题需要分三个零点,也就是四个部分)
|x+6|+|x-2|+|x-6|+|x+2|(提示:四个零点)
不要怕麻烦,零点分段法的精髓就是分类讨论!
思考题:
|x|+|x+1|+|x+2|+……+|x+n|
已知n为奇数,且当mxm+1时原式化简后为一定值(意思是在mxm+1这个区间中x取何值,原式的值都不变),求m的值。
提示:想想刚才讲零点分段法分成三个部分时的第2段,所有x全都消掉了,最后出现的是10这个定值!所以如何才能消掉所有的x呢?
以上就是(零点分段法)全部内容,收藏起来下次访问不迷路!