数轴标根法
数轴标根法
第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。(注意:一定要保证x前的系数为正数)
例如:将x3-2x2-x+20化为(x-2)(x-1)(x+1)0
第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1
第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2
第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“”,则取数轴上方,穿根线以内的范围;如果不等号为“”则取数轴下方,穿根线以内的范围。x的次数若为偶数则不穿过,即奇过偶不过。
例如:
若求(x-2)(x-1)(x+1)0的根。
在数轴上标根得:-1 1 2
画穿根线:由右上方开始穿根。
因为不等号为“”则取数轴上方,穿跟线以内的范围。即:-1x1或x2。(如下图所示)
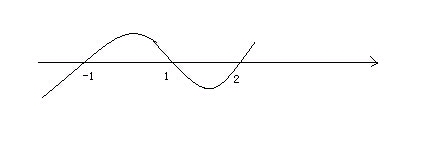
例题
注意事项
运用序轴标根法解不等式时,常犯以下的错误:
1. 出现形如(a-x)的一次因式时,匆忙地“穿针引线”。
例1 解不等式x(3-x)(x+1)(x-2)0。
解 x(3-x)(x+1)(x-2)0,将各根-1、0、2、3依次标在数轴上,由图1可得原不等式的解集为{x|x-1或0x2或x3}。
事实上,只有将因式(a-x)变为(x-a)的形式后才能用序轴标根法,正确的解法是:
解 原不等式变形为x(x-3)(x+1)(x-2)0,将各根-1、0、2、3依次标在数轴上,原不等式的解集为{x|-1x0或2x3}。
2. 出现重根时,机械地“穿针引线”
例2 解不等式(x+1)(x-1)2(x-4)30
解 将三个根-1、1、4标在数轴上,原不等式的解集为{x|x-1或1x4}。
这种解法也是错误的,错在不加分析地、机械地“穿针引线”。出现几个相同的根时,所画的浪线遇到“偶次”点(即偶数个相同根所对应的点)不能过数轴,仍在数轴的同侧折回,只有遇到“奇次”点(即奇数个相同根所对应的点)才能穿过数轴,正确的解法如下:
解 将三个根-1、1、4标在数轴上,画出浪线图来穿过各根对应点,遇到x=1的点时浪线不穿过数轴,仍在数轴的同侧折回;遇到x=4的点才穿过数轴,于是,可得到不等式的解集
{x|-1x4且x≠1}
3. 出现不能再分解的二次因式时,简单地放弃“穿针引线”
例3 解不等式x(x+1)(x-2)(x3-1)0
解 原不等式变形为x(x+1)(x-2)(x-1)(x2+x+1)0,有些同学同解变形到这里时认为不能用序轴标根法了,因为序轴标根法指明要分解成一次因式的积,事实上,根据这个二次因式的符号将其消去再运用序轴标根法即可。
解 原不等式等价于
x(x+1)(x-2)(x-1)(x2+x+1)0,
∵ x^2+x+10对一切x恒成立,
∴ x(x-1)(x+1)(x-2)0,由图4可得原不等式的解集为{x|x-1或0x1或x2}
以上就是(数轴标根法)全部内容,收藏起来下次访问不迷路!