形象表示矩阵的秩的由来

形象表示矩阵的秩的由来

概念：

mxn

1阶子式是单个元素，显然满足“至少一个不为0”

2阶子式，只要找到一个不为零即可

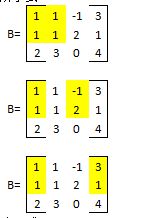
找一个不为0

3阶子式

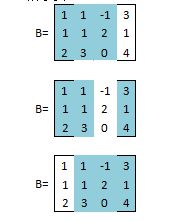
3阶子式全为0，所以r（B）=2

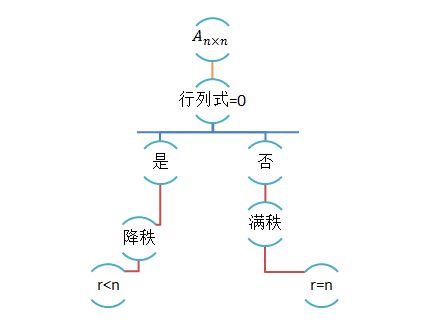
nxn

1阶子式显然满足“至少一个不为0”

2阶子式

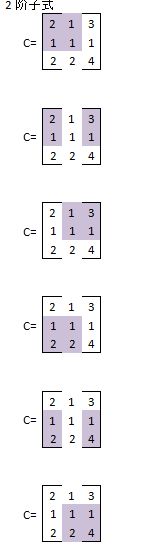
3阶子式

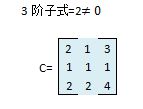
满秩矩阵行列式不为零

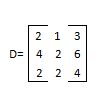
1阶子式显然满足“至少一个不为0”

2阶子式

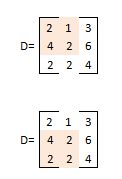
3阶子式

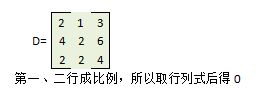
降秩矩阵行列式为0

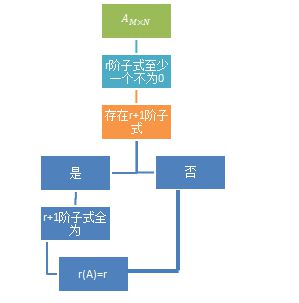
秩的本质是方程组约束条件个数，即初等行变换阶梯化后的非0行数目。

考点：初等行变换

（形象表示矩阵的秩的由来）宝，都看到这里了你确定不收藏一下？？