反三角函数值域(三角函数和反三角函数的之间的关系和定义域、值域吗？)

反三角函数值域(三角函数和反三角函数的之间的关系和定义域、值域吗？)

首先，我们来看看有哪些三角函数，正弦函数sin , 余弦函数cos ，正切函数 tan ，余切函数cot ，正割函数sec ,余割函数csc 。

接下来，我们来看看有哪些反三角函数，反正弦函数arcsin ，反余弦函数 arccos ,反正切函数arctan ，反正割函数 arcsec , 反余割函数 arccsc 。

继续。我们来看看它们之间的关系。

反三角函数和三角函数互为反函数。一般来说，设函数y=f x x∈A的值域是C，若找得到一个函数g y在每一处g y都等于x，这样的函数x= g y y∈C叫做函数y=f x x∈A的反函数，记作x=f-1 y 。反函数x=f -1 y的定义域是函数y=f x的值域，反函数x=f -1 y的值域是函数y=f x的定义域。正函数与反函数的图像是关于y=x对称，最具有代表性的互为反函数就是对数函数与指数函数。有关反函数的内容下次具体讨论。三角函数的之间关系：三角形函数的关系可以用六边形表示，如图1所示。

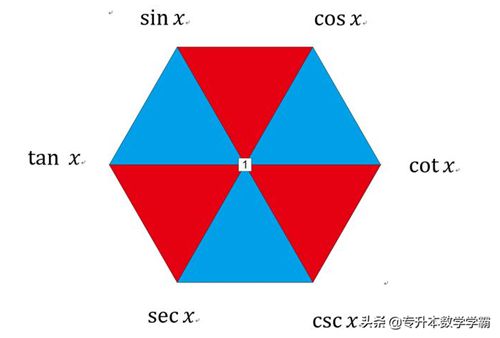
图1 三角函数的六边形法则

①平方关系，在六边形中，红色区域的倒三角形成平方关系。

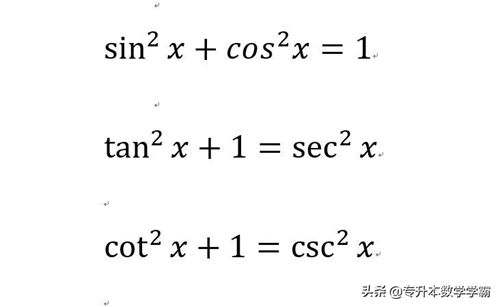
图2 平方关系

②比值关系，在六边形中，任意一点的值是前面相邻两个函数的比值。

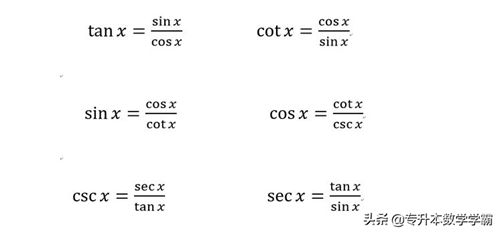
图3 比值关系

③倒数关系，在六边形中，六边形的对角线的两个三角函数成倒数关系。

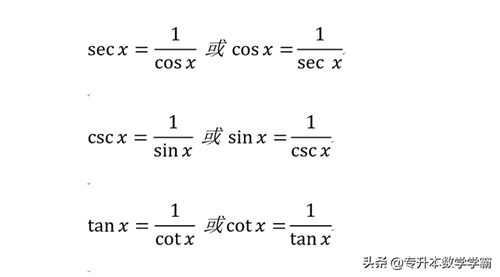
图4 倒数关系

④ 乘积关系，在六边形中 任意一点的值等于紧挨着这一点的两个端点值 的积

图5 乘积关系

3.三角函数的定义域：

我们一起分别来讨论它们的定义域和值域：

①正弦函数sin 的定义域是一切实数R，值域是[-1,1]，其函数图象如图6所示：

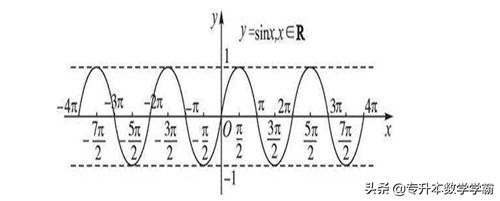
图6 正弦函数图像

由图象可知，正弦函数是奇函数，周期 T=2，其对称性是关于原点对称，单调性：单调递增区间：[-/22k，/22k] ， K∈Z ；单调递减区间：[/22k，3/22k]， K∈Z。正弦函数的定义域是反正弦函数的值域，正弦函数的值域是反正弦函数的定义域。

②余弦函数cos 的定义域是一切实数R，值域是[-1,1],其函数图象如图7所示：

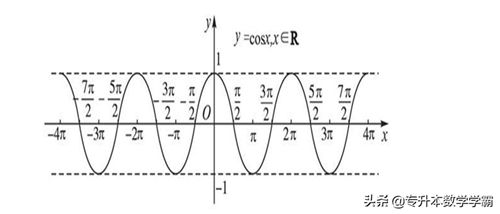
图7 余弦函数图像

由图象可知，余弦函数是偶函数，周期 T=2，其对称性是关于y轴对称，单调性：单调递增区间：[2k，22k] ， K∈Z 单调递减区间：[02k，2k]， K∈Z。余弦函数的定义域是反余弦函数的值域，余弦函数的值域是反余弦函数的定义域。

③正切函数 tan 的定义域是 ≠ /2+k， K∈Z，值域是一切实数R，其函数图像如图8所示：

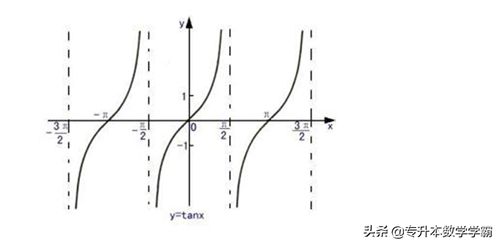
图8 正切函数图像

由图象可知，正切函数是奇函数，周期 T=，其对称性是关于原点对称，单调性只有单调递增，单调递增区间为[-/2k，/2k] ， K∈Z，没有单调递减。正切函数的定义域是反正切函数的值域，正切函数的值域是反正切函数的定义域。

④ 余切函数cot 的定义域是 ≠k， K∈Z 值域是一切实数R，其函数图象如图9所示：

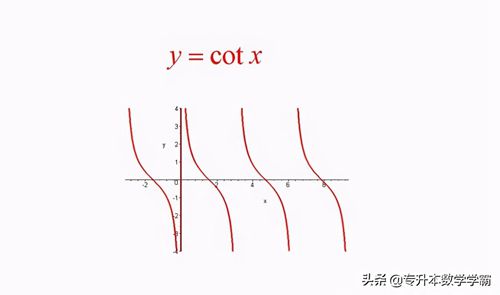
图9 余切函数图像

由图像可知，余切函数是奇函数，周期 T=，其对称性是关于原点对称，单调性只有单调递减，单调递减区间为[0k，k] ，没有单调递增。余切函数的定义域是反余切函数的值域，余切函数的值域是反余切函数的定义域。

由于正割函数sec 、余割函数csc 、反正割函数arcsec 、反余割函数arccsc ，专升本数学不考，加上正割函数、余割函数、反正割函数、反余割函数的图像麻烦，就不进行研究了。

今天的讨论到此为止，以上内容是我个人见解，不代表官方的意见，下次我们来讨论其他函数的五种性质：单调性、奇偶性、对称性、周期性、有界无界性。

以上就是（反三角函数值域(三角函数和反三角函数的之间的关系和定义域、值域吗？)）全部内容，收藏起来下次访问不迷路！