配方法解一元二次方程(解一元二次方程的配方法)

配方法解一元二次方程(解一元二次方程的配方法)

本文学习配方法解一元二次方程。

准备知识：完全平方式；二次根式的化简；解方程的移项、合并、系数化为1.

一、什么是完全平方式

1.形如a+2ab+b或a+2ab+b的式子叫做完全平方式。

2.完全平方式的特征：

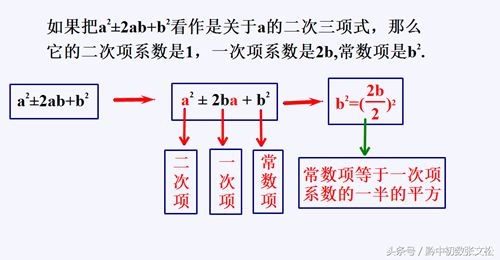
3.练习：在下列横线上填入适当的数使等式成立

1x+6x+_____ = x+__ ； 2 y-2y+____= y-___； 3z+z+___= z+___.

二、配方法

1.我们已经知道，用直接开平方法可以解以下类型的方程：

1ax=0 b、c皆为0； 2ax+c=0 b=0； 3a x+b=c. bc均不为0

结论：在方程ax+bx+c=0 a≠0中，当b=0时，都可以用直接开平方法来解。当b≠0时，含未知数部分必须是关于未知数的一次式的平方，才能用直接开平方法来解。

自然想到的问题是：不是完全平方式的怎么做？

2.转化思想是学习和研究数学的一种重要的思想方法。

比如

我们已经会用直接开平方法解方程 x-3=0，那么怎样解方程x-6x+9=0呢？

注意观察，我们发现利用完全平公式，可以将x-6x+9转化为 x-3.进而把方程x-6x+9=0转化为方程 x-3=0来解。

再比如，我们会解 x-3=4，那我们怎么解 x-6x+5=0呢？

通过观察，将方程x-6x+5=0两边同时加上4，得x-6x+9=4.

此时，方程的左边正好是完全平方式。分解得 x-3=4。

这样就把方程x-6x+5=0转化为 x-3=4，从而找到解方程的途径。

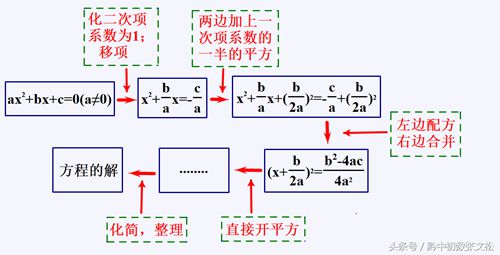
3.像上面那样，将方程通过变形，使含未知数的部分变为完全平方式，然后，再用直接开平方法解方程的方法叫做配方法。

直接开平方法的步骤：

4.举例：

1二次项系数为1

2二次项系数不为1

关键：当二次项系数为1 不为1时，一般要先化为1时，方程两边同时加上一次项系数的一半的平方。

以上就是（配方法解一元二次方程(解一元二次方程的配方法)）全部内容，收藏起来下次访问不迷路！