直角三角形三角函数

直角三角形三角函数

在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中∠ACB为直角。对∠BAC而言，对边a=BC、斜边c=AB、邻边b=AC，则存在以下关系：

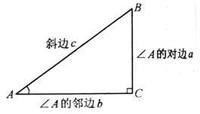
直角三角形ABC

基本函数缩写表达式语言描述

正弦函数sina/c∠A的对边比斜边

余弦函数cosb/c∠A的邻边比斜边

正切函数tana/b∠A的对边比邻边

余切函数cotb/a∠A的邻边比对边

正割函数secc/b∠A的斜边比邻边

余割函数cscc/a∠A的斜边比对边

正弦值在

随角度增大（减小）而增大（减小），在

随角度增大（减小）而减小（增大）；

余弦值在

随角度增大（减小）而增大（减小），在

随角度增大（减小）而减小（增大）；

正切值在

随角度增大（减小）而增大（减小）；

余切值在

随角度增大（减小）而减小（增大）。

特殊角：

tan15=2-√3

cot15=2+√3

sin30=0.5

cot30=√3

cos30=（√3）/2

tan30=（√3）/3

tan45=1

cot45=1

sin45=（√2）/2

cos45=（√2）/2

……

两角和与差

证明：

取直角坐标系，作单位圆；取一点A，连接OA，与X轴的夹角为α； 取一点B，连接OB，与X轴的夹角为β， 则OA与OB的夹角即为α-β

∵A（cosα,sinα），B （cosβ,sinβ），O（0,0）

∴OA=（cosα,sinα），OB=（cosβ,sinβ）（向量）

∴OA·OB=|OA| |OB| cos （α-β） =cos α cos β + sin α sin β

∵|OA| = |OB| = 1

∴cos（α-β）=cosαcosβ+sinαsinβ

取β=-β，可得cos（α+β）=cosαcosβ-sinαsinβ

万能公式

sina=[2tan（a/2）]/[1+tan²（a/2）]

cosa=[1-tan²（a/2）]/[1+tan²（a/2）]

tana=[2tan（a/2）]/[1-tan²（a/2）]

泰勒展开式

泰勒展开式又叫幂级数展开法

泰勒展开式正弦定理

对于边长为a,b和c而相应角为A,B和C的三角形，有：

sinA / a = sinB / b = sinC/c

余弦定理

对于边长为a、b、c而相应角为A、B、C的三角形，有：

a² = b² + c²- 2bc·cosA

b² = a² + c² - 2ac·cosB

c² = a² + b² - 2ab·cosC

正切定理

对于边长为a,b和c而相应角为A,B和C的三角形，有：

记忆口诀

三角函数是函数，象限符号坐标注。函数图像单位圆，周期奇偶增减现。

同角关系很重要，化简证明都需要。正六边形顶点处，从上到下弦切割；

中心记上数字一，连结顶点三角形。向下三角平方和，倒数关系是对角，

顶点任意一函数，等于后面两根除。诱导公式就是好，负化正后大化小，

变成锐角好查表，化简证明少不了。二的一半整数倍，奇数化余偶不变，

将其后者视锐角，符号原来函数判。两角和的余弦值，化为单角好求值，

余弦积减正弦积，换角变形众公式。和差化积须同名，互余角度变名称。

计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。

逆反原则作指导，升幂降次和差积。条件等式的证明，方程思想指路明。

万能公式不一般，化为有理式居先。公式顺用和逆用，变形运用加巧用；

一加余弦想余弦，一减余弦想正弦，幂升一次角减半，升幂降次它为范；

三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围；

利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集。

若对数学有兴趣，请关注我，我每天都会投稿有关数学的专栏[doge]PS：若本文有错误的地方，请私发给我，我再进行修改。

（直角三角形三角函数）宝，都看到这里了你确定不收藏一下？？