内角平分线定理的六种证明方法（续前篇） (内角平分线定理的逆定理)

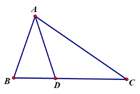
证法（4）：

延长BA，在延长线上取一点E，使AE=AC，连接EC，如下图

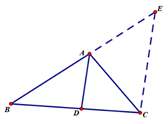
∵AE=AC

∴∠E=∠ACE

∵∠BAD=∠CAD，∠BAC=∠E+∠ACE

∴∠E=∠BAD

∴AD∥CE

由平行线分线段成比例的性质得：

AB/AE=BD/CD=AB/AC

证法（5）：

过D点作AC的平行线，交AB于E点，如下图

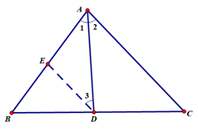
∴∠1=∠2=∠3，AE=ED

由平行线分线段成比例的性质得：BE/AE=BD/CD

∴BE/ED=BD/CD

而BE/ED=AB/AC(相似三角形的性质）

∴BD/CD=AB/AC

证法（6）：

作△ABC 的外接圆O，延长AD交圆O于E点，连接EC

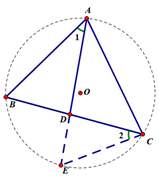
∵同弧所对圆周角相等

∴∠1=∠2，∠B=∠E

∴△BAD∽△ECD

所以AB/CE=BD/ED...①

∵∠EAC=∠2，∠E=∠E

∴△EAC∽△ECD

∴EC/ED=AC/CD...②

由①②可得：AB/AC=BD/CD

本来是要整理正弦定理的证法的，但是上次的专栏里有人评论了一个很好的方法，也就是证法（4），在那个方法的指导下我又想到了另外两种方法，为了内容上的连续性，我就先发这篇了。昨天其实发过了，但是出了点错，下次发布专栏一定要好好检查一下。

以上就是（内角平分线定理的六种证明方法（续前篇） (内角平分线定理的逆定理)）全部内容，收藏起来下次访问不迷路！