海明码（HammingCode） (海明码(Hamming Code) 是一种( ))

海明码（HammingCode） (海明码(Hamming Code) 是一种( ))

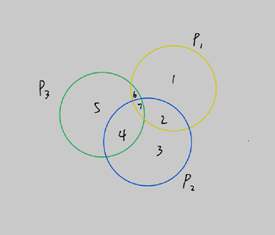
Px代表组号 1、2、3.....表示数据

如上图所示，如果我们知道P1、P2组出错了 P3组没错，那么显而易见2这个数据出错了。同理，如果P1、P3出错了而P2没错，则可确定数据6出错了。而如果P1、P2、P3都出错了，则可了解数据7出错了。由于采用的是二进制，所以直接对错误数据进行取反操作即可。这里要注意的是，海明码默认数据最多只错一个（因为这是最常见的错误）

那么数据是如何来划分的呢？ （K个校验码对应K个分组）

首先要确实校验码的个数，假设有K个校验码，则能表示2^K个状态。设数据为N,则N+K位都可能出错（校验码也能出错)，所以2^K=N+K+1（我们有N+K位可能出错，这个1表示无错的情况，在满足这个不等式的情况下K要取最小值)。

其次，在确定校验码的个数后，还要确定它们的位置。校验码都是放在2^x位置上，如1、2、4、8....... 如原数据1101要插入三个校验码则为 110a1ba(ab为校验码，位置从右往左数）

然后我们来分组，海明码的分组首先将位置1、2、3、4......十进制数转换成二进制0001、0010、0011、0100......然后P1组包括xxx1的所有位置数，P2组保持xx1x的所有位置数,以此类推。位置数为1,3,5,7,9,11......的数据进到P1组;2,3,6,7,10,11......的数据进到P2组;4,5,6,7的数据进到P3组......。

确定好分组后，通过偶校验确定每个组对应的校验码的值，P1对应第一个位置（1）的校验码,P2对应第二个位置(2)的校验码，P3对应第三个位置(4)的校验码。举个例子如果P1中有奇数个1则处于位置1的第一个校验码的值为1。P3中有偶数个1则处于位置4的第三个校验码的值为0。

接受方怎么定位错误呢？

上面我们将的都是发送方做的事情，接受方该如何检错、纠错？其实很简单，对每个分组分别进行校验（默认偶校验），错的记1，对的记0。这样假如三个分组 第一组第二组出错则为011，表示位置3上的数据出错了，那么我们只需要对这个位置上的数取反即可。为什么这里第一组和第二组出错我们能直接定位到位置3呢？其实就是最上面图代表的思想。经过上面的设计我们将位置数由十进制转换成了2进制，并根据位的权重（xx1、x1x、1xx)进行了分组。然后我们对每个组，进行校验得出的结果，实际上就是在找出错值的位置。例如，P1（xx1）出错了权重为1的位确定了为1（P1出错表示这个数在P1内），P2（x1x）出错权重位2的位确定了为1，P3没错，权重位4的位置确定了为0，所以最后就找出011对应的十进制数3位置出错了。

以上就是（海明码（HammingCode） (海明码(Hamming Code) 是一种( ))）全部内容，收藏起来下次访问不迷路！